Improved Bounds on the Epidemic Threshold of Exact SIS Models on Complex Networks
N. Azizan R., C. Thrampoulidis, and B. Hassibi
Proceedings of the IEEE Conference on Decision and Control (CDC), 2016 (Invited Paper)
[pdf] [cite]
The SIS (susceptible-infected-susceptible) epidemic model on an arbitrary network, without making approximations, is a 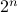 -state Markov chain with a unique absorbing state (the all-healthy state). This makes analysis of the SIS model and, in particular, determining the threshold of epidemic spread quite challenging. It has been shown that the exact marginal probabilities of infection can be upper bounded by an -state Markov chain with a unique absorbing state (the all-healthy state). This makes analysis of the SIS model and, in particular, determining the threshold of epidemic spread quite challenging. It has been shown that the exact marginal probabilities of infection can be upper bounded by an 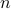 -dimensional linear time-invariant system, a consequence of which is that the Markov chain is ‘‘fast-mixing’’ when the LTI system is stable, i.e. when -dimensional linear time-invariant system, a consequence of which is that the Markov chain is ‘‘fast-mixing’’ when the LTI system is stable, i.e. when 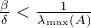 (where (where 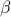 is the infection rate per link, is the infection rate per link, 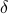 is the recovery rate, and is the recovery rate, and 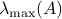 is the largest eigenvalue of the network's adjacency matrix). This well-known threshold has been recently shown not to be tight in several cases, such as in a star network. In this paper, we provide tighter upper bounds on the exact marginal probabilities of infection, by also taking pairwise infection probabilities into account. Based on this improved bound, we derive tighter eigenvalue conditions that guarantee fast mixing (i.e., logarithmic mixing time) of the chain. We demonstrate the improvement of the threshold condition by comparing the new bound with the known one on various networks with various epidemic parameters. is the largest eigenvalue of the network's adjacency matrix). This well-known threshold has been recently shown not to be tight in several cases, such as in a star network. In this paper, we provide tighter upper bounds on the exact marginal probabilities of infection, by also taking pairwise infection probabilities into account. Based on this improved bound, we derive tighter eigenvalue conditions that guarantee fast mixing (i.e., logarithmic mixing time) of the chain. We demonstrate the improvement of the threshold condition by comparing the new bound with the known one on various networks with various epidemic parameters.
|