SIRS Epidemics on Complex Networks: Concurrence of Exact Markov Chain and Approximated Models
N. Azizan R. and B. Hassibi
Proceedings of the IEEE Conference on Decision and Control (CDC), 2015 (Invited Paper)
[pdf] [cite]
We study the SIRS (Susceptible-Infected-Recovered-Susceptible) spreading processes over complex networks, by considering its exact 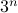 -state Markov chain model. The Markov chain model exhibits an interesting connection with its -state Markov chain model. The Markov chain model exhibits an interesting connection with its 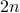 -state nonlinear ‘‘mean-field’’ approximation and the latter's corresponding linear approximation. We show that under the specific threshold where the disease-free state is a globally stable fixed point of both the linear and nonlinear models, the exact underlying Markov chain has an -state nonlinear ‘‘mean-field’’ approximation and the latter's corresponding linear approximation. We show that under the specific threshold where the disease-free state is a globally stable fixed point of both the linear and nonlinear models, the exact underlying Markov chain has an 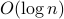 mixing time, which means the epidemic dies out quickly. In fact, the epidemic eradication condition coincides for all the three models. Furthermore, when the threshold condition is violated, which indicates that the linear model is not stable, we show that there exists a unique second fixed point for the nonlinear model, which corresponds to the endemic state. We also investigate the effect of adding immunization to the SIRS epidemics by introducing two different models, depending on the efficacy of the vaccine. Our results indicate that immunization improves the threshold of epidemic eradication. Furthermore, the common threshold for fast-mixing of the Markov chain and global stability of the disease-free fixed point improves by the same factor for the vaccination-dominant model. mixing time, which means the epidemic dies out quickly. In fact, the epidemic eradication condition coincides for all the three models. Furthermore, when the threshold condition is violated, which indicates that the linear model is not stable, we show that there exists a unique second fixed point for the nonlinear model, which corresponds to the endemic state. We also investigate the effect of adding immunization to the SIRS epidemics by introducing two different models, depending on the efficacy of the vaccine. Our results indicate that immunization improves the threshold of epidemic eradication. Furthermore, the common threshold for fast-mixing of the Markov chain and global stability of the disease-free fixed point improves by the same factor for the vaccination-dominant model.
|